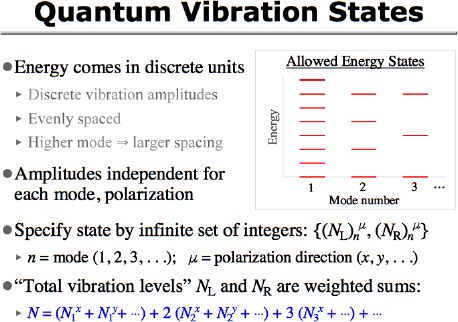
One of the main implications of quantum mechaincs for us is that energy comes in discrete units. So in particular, only a certain discrete set of vibrational amplitudes are allowed; they turn out to be evenly spaced (that is, all of the discrete units of energy are the same size). And since higher harmonic modes correspond to more wiggling, the units of energy for them are larger, too.
Because all of the different modes and polarizations are independent (for both left-moving and right-moving vibrations separately), we have to specify the amplitude for each one. That means that the whole quantum mechanical state of the string can be specified by specifying the (integer) number of energy units in each mode: an infinite set of integers.
For our purposes later, we'll mainly be concerned with the total amount of vibrational energy in waves traveling each direction around the string (the left-moving and right-moving totals). Because of the different energy level spacings, those totals end up being proportional to a weighted sum of the integers describing the quantum state.
Up to my research page.
Up to my professional page.
My personal site is also available.
Any questions or comments? Write to me: jensens@alma.edu
Copyright © 2004 by Steuard Jensen.